Alas, for any particular i and n, the set V_i, n is at most countable, because distinct points (x, 0) and (y, 0) of one V_i, n must lie at least 2/n apart, as measured by |x – y|. Indeed, whatever the points (x, 0) and (y, 0) of V_i, n , the one thing that is certain about the value |x – y| is that, of the three classically exhaustive possibilities

	|x – y|	= 0 ,
0 <	|x – y|	< 2/n ,
	|x – y|	> 2/n ,

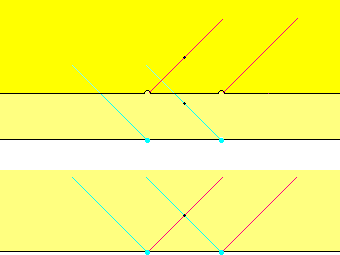
only the first and third can subsist; for, were the second the case, the section f must send the point at which the two intersecting fingers meet, as the illustrations show, to a point in the double cover that lies at once in both of the broken open Vs shown, which is impossible, as those two broken open Vs are disjoint.

[ >> ]