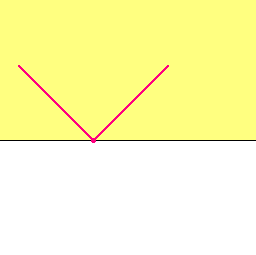
Heath’s V-space is just the upper half-plane, with an unusual topology,
in which all points above the x-axis are open, and the basic open neighborhoods of a point (x, 0) on
the x-axis are ... the various symmetric “open V ”s, with 45-degree fingers of arbitrary
equal non-zero lengths, as shown.
(These are just the images of the vertical symmetric basic open
neighborhoods of (x, 0) in Rdiscrete × Rmetric
under the quotient map (x, y) ·-·-·>
(x+y, |y|) .)
Notation:
Vε(x) = {(x+r, |r|) :
0 < r < ε}
(ε > 0, x ∈ R).
[ >> ]