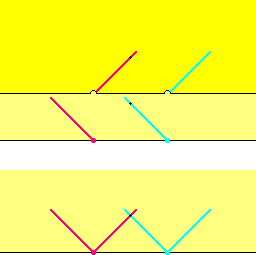
Distinct reals x, y in X_ε^λ must lie at least 2ε apart: |x - y| > 2ε. For if instead 0 < |x – y| < 2ε , then f(V_ε(x) ∩ V_ε(y)) ⊂ V_ε^λ(x) ∩ V_ε^λ(y) = ∅,  while V_ε(x) ∩ V_ε(y) = {((x+y)/2, |x-y|/2)} ≠ ∅. 
  Thus each X_ε^λ is at most countable, as claimed, and so, therefore, is
X = ∪{X_1/n⁰ : n > 0} ∪ ∪{X_1/n¹ : n > 0} . [ >> ]